However, the UNSCEAR report merely states that it “does not recommend,” which isn’t the same as declaring it will regulate what “can be said.” The unidentified author of the post seems to be inferring that the UNSCEAR controls who says what about the radiation effects.
Conca, in the Forbes article, takes it one step further, by placing the statement below the “official” UNSCEAR logo: “The United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) has finally admitted that we can’t use the LNT (linear no-threshold dose) hypothesis to predict cancer from low doses of radiation. Now the Japanese people can start eating their own food again and stop being as afraid. Source: United Nations.” This juxtaposition of his opinion next to the UNSCEAR logo could easily make readers misconstrue that the statement is the official statement by the UNSCEAR.
As for Conca’s claim that radiation doses less than 10 rem (0.1 Sv) are “no big deal” and that
“the linear no-threshold dose hypothesis does not apply to doses less than 10 rem (0.1 Sv), which is the region encompassing background levels around the world,” it simply is a mystery how he seems to have reached such a conclusion, seemingly straight out of thin air.
First, nowhere in the UNSCEAR document he links to, “UN document A/67/46,” does it mention 10 rem (0.1 Sv) as “no big deal” or applying to “the region encompassing background levels around the world.” However, the paragraph 25(f) excerpted above does refer to “chronic exposure to radiation at levels that are typical of the global average background levels of radiation.” Is it possible that he took a liberal interpretation of “the global average background levels of radiation” to mean the highest background levels in rare locations, HBRAs, such as Ramsar, Iran?
According to paragraph 92 on page 111 of UNSCEAR 2000 Annex B: Exposures from natural radiation sources, “worldwide annual exposures to natural radiation sources would generally be expected to be in the range 1-10 mSv, with 2.4 mSv being the present estimate of the central value.”
Secondly, radiation doses less than 10 rem (0.1 Sv or 100 mSv) are not a “no big deal” situation as claimed by Conca. The 2012 meta-analysis by evolutionary biologists Anders Moller (France) and Timothy Mousseau (United States), “The effects of natural variation in background radioactivity on humans, animals and other organisms,” found evidence of significant effects of natural variation in background radiation on mutation rates, DNA damage/repair, immunology and disease including cancer.
Radiation effects from exposures well below 10 rem (0.1 Sv or 100 mSv), including background radiation, medical exposure, leukemias in Chernobyl clean-up workers as well as leukemias near nuclear power stations, are discussed by the British radiation biologist, Ian Fairlie.
Thirdly, it is untrue that the LNT hypothesis does not apply to doses below 10 rem (0.1 Sv or 100 mSv). Fairlie discusses very large studies with statistically significant results at very low doses, even down to background levels, showing the linear shape of the dose response relationship down to low doses.
Contrary to Conca’s claim that Japan cut the accepted global limit of 1,000 Bq/kg cesium level in half hoping it would have a calming influence on public’s radiation fear, Japan actually already had guidelines established to be used in case of emergency. So the initial regulatory limit of 500 Bq/kg of cesium was not a compromise by the Japanese government for the purpose of “easing” the public fear. It has now been lowered to 100 Bq/kg. The U.S. regulatory limit is outrageously high at 1,200 Bq/kg. This means any radiation tests conducted on Japan imports in the United States immediately after the accident were practically useless, even though the result might have been below the derived intervention level (DIL) of 1,200 Bq/kg.
Besides, the current regulatory limit for milk Conca mentioned in his article is not even accurate in that it is not 200 Bq/kg, but 50 Bq/kg.
The statement, “Accepted global limits on radioactivity levels in foods is 1,000 Bq/kg (1,200 Bq/kg in the U.S.),” is a little misleading in terms of who “accepts” these numbers. These high numbers are apparently set by those interested in protecting and promoting advancement of nuclear energy and imposed upon people who don’t really even know what the numbers mean. On the other hand, those whose interests lie in protecting physical well-being and lives of people, apparently have other perspectives, such as not accepting these limits of 1,000 and 1,200 Bq/kg.
The primary fact is that there is no dose of radiation that is recognized to be harmless, as excerpted from the report, “Calculated Fatalities from Radiation.”
“Setting official maximum levels of radionuclides to be tolerated in food is supposed to protect the population from danger. But, in contrast to chemical toxins, there is no threshold below which radioactivity is harmless. Thus there is also no dose of radiation, no matter how small, that is harmless, benign or unobjectionable. The authority (government or international organization) that recommends or sets standards, or maximum permissible value limits, basically decides on how many fatalities or cases of illness will be acceptable in a given situation.”
In fact, foodwatch, an European consumer rights group, and International Physicians for the Prevention of Nuclear War (IPPNW) Germany called for lowering of the permissible limits of radioactive cesium to 8 Bq/kg for baby food and 16 Bq/kg for all other foods, based on the maximum annual effective radiation dose of 0.3 mSv, which is the maximum exposure limit set out in Germany’s radiation protection legislation for normal operations in nuclear power plants.
Based on Conca’s statements in the comment section of his article, he seems to think a “little bit of cesium ingested” is harmless as it is excreted from the body. But is it really harmless? Does radioactive cesium simply get distributed to mostly muscles, as generally recognized, and eventually excreted without doing any harm?
An exiled Belarusian anatomical pathologist Bandazhevsky, now living in Ukraine, showed that radioactive cesium accumulated in various organs in the body, other than skeletal muscles. He claimed that radioactive cesium affected multiple organ systems, especially cardiac muscles, causing arrhythmia and sudden cardiac deaths.
In the study published on January 23, 2013, “Artificial Radionuclides in Abandoned Cattle in the Evacuation Zone of the Fukushima Daiichi Nuclear Power Plant,” a team of Japanese researchers showed how cesium accumulated in various organs of cows.
We have no way of knowing if the accumulated cesium would have eventually caused cancer in these cows, or if they were physically ill before euthanized according to the government order to kill animals left behind in the evacuation zone. However, it is a little hard to imagine the accumulated radioactive cesium causing no harm in delicate cells and tissues of these organs, such as heart, kidney, liver, lungs, bladder, thyroid, etc.
Conca states that as UNSCEAR found no observable health effects from the Fukushima nuclear accident, the Japanese people can start eating their own food again and moving back into areas only lightly contaminated with radiation levels that are similar to background in many areas of the world.
According to paragraph 8 on page 4 of the UNSCEAR report, “UN document A/67/46,” sources of data for the Committee’s evaluation included the Japanese government, United Nations Member States, and other organizations such as the Comprehensive Nuclear-Test-Ban Treaty Organization, the Food and Agriculture Organization of the United Nations (FAO), the International Atomic Energy Agency (IAEA), the World Health Organization (WHO) and World Meteorological Organization (WMO). They also used information and analyses published in peer-reviewed scientific journals as well as measurements uploaded by the public on crowdsourcing websites.
As the UNSCEAR only considers cancer and heritable effects important in establishing radiation risk estimates for low dose exposures, it is not surprising that they concluded that
“No health effects have been attributed to radiation exposure observed among workers or children or any other members of the population.” in paragraph 9(a). At 22 months after the accident, it is considered too soon for radiation-induced cancer to develop, and Japanese government and Fukushima Prefecture do not seem to be actively conducting epidemiological studies in showing heritable effects such as congenital deformities.
However, in reality, there are unofficial accounts of birth defects such as anencephaly and leukemia, not only in Fukushima Prefecture but also in Tokyo and the Kanto region surrounding Tokyo. In addition, a variety of symptoms such as nosebleeds, rash, fatigue, and spread as well as recurrence of infections have been reported in Tokyo and the Kanto region, in addition to increased incidence of abnormal EKG in school children in some areas. Reports of thyroid disorders, such as Hashimoto’s disease and subacute thyroiditis are heard more frequently. Leukopenia has been reported in children in Tokyo and the Kanto region.
TEPCO workers and external contractors involved in the on-site clean-up activities are not reported to have any health effects, but there are no studies or data published to back up that claim. In other words, we have no objective evidence that no health effects have occurred to those workers. There have been at least 5 workers who have died since the accident, with the last reported death being from August 2012, and in some cases their causes of death were not revealed by TEPCO, citing privacy protection. Other than these five, two other TEPCO employees were found dead in the reactor 4 turbine building.
It is not clear where Conca derived information in the following clause, “Radiation played no role in the coincidental deaths of six Fukushima workers in the time since the accident, who died from accidents, e.g. being crushed by debris or being swept out to sea.” Insinuating, without any concrete evidence, that six workers died from accidents is absurd - are there videotapes or eye witness reports to corroborate his claim? Does he honestly know what "really" happened in Japan after the earthquake and tsunami?
The first worker to die was a 60-year-old man who died of “heart attack” on his second day of work. He was one of many “seasonal nuclear power plant workers” who would go to various nuclear power plants on demand. These workers might not know what their cumulative radiation exposure doses are. Sudden cardiac deaths are often called “heart attacks.” In view of this, this man’s “heart attack” could be the result of long-term exposure.
A worker in his 40’s died of acute leukemia in mid-August, 2011, after working at Fukushima Dai-ichi NPP for one week in the beginning of August. His exposure dose was supposedly 0.5 mSv, and TEPCO denied any relationship between his leukemia and radiation. It was not known if he might have had any other occupational radiation exposure prior to his work at Fukushima Dai-ichi, but TEPCO had no intention of investigating his death any further.
Another worker whose circumstance of death has been publicized, was a 57-year-old man who was found unconscious as he was resting after not feeling well on August 22, 2012. He was dead on arrival at the hospital. After working at Fukushima Dai-ichi for one year, his cumulative dose was 25 mSv.
Paragraph 9(e) mentions thyroid monitoring, which was conducted on 1,083 children (544 boys and 539 girls) in Iitate village, Kawamata town and Iwaki-city in late March, 2011, showing no individual exceeding a screening level of 0.2 μSv/h that was derived from a thyroid dose of 100 mSv.
The following is excerpted from the proceedings of the United Nations Sixty-seventh General Assembly Fourth Committee, which was held on November 13, 2012.
“Maximum dose reported was ‘35 mSv,’ which , he said, was reassuring, because that was significantly lower than what had been observed after the Chernobyl incident. ‘That good news must be underlined,’ asserted the representative of Argentina.”
This thyroid screening was done on March 26-27, 2011 in Iwaki-city, on March 28-30, 2011 in Kawamata town, and on March 29-30, 2011 in Iitate village. In Iitate village, the background radiation level was so high, over 10 μSv/h in some cases, and they had to scurry around to find almost a cubby-hole like area in a city hall with a background level of 0.2 μSv/h, where 300 children were screened. For the whole group including Iitate village children, 55% was 0 μSv/h and 26% was 0.01 μSv/h, and 99% was under 0.04 μSv/h. The highest was 0.1 μSv/h. Under such high background conditions, can accurate measurements verifiably be conducted?
Nevertheless, the most recently published results of the thyroid ultrasound examination, conducted as part of the Fukushima Prefecture Health Management Survey, shows 38,327 (39.9%) of 95,954 children with abnormalities. There are about 360,000 children in Fukushima Prefecture, and the initial round of the ultrasound examination is still ongoing.
Although Conca wrote in the Forbes article, “UNSCEAR also found no observable health effects from last year’s nuclear accident in Fukushima. No effects,” truth might be far from it.
With due respect, the studies by WHO and Tokyo University which Conca refers to, apparently excerpted from his favorite source, the World Nuclear News post, might not reflect accurate information, although exactly which studies he is referring to is unclear. If it is WHO’s “Preliminary Dose Estimation from the nuclear accident after the 2011 Great East Japan Earthquake and Tsunami” that he is referring to, it was most likely based on official information from the Japanese government. http://www.who.int/ionizing_radiation/pub_meet/fukushima_dose_assessment/en/index.html
The Japanese government did issue an evacuation order for the 20-km zone, but the actual evacuation process was chaotic, and in some cases people went in the direction of the radioactive plume as the government failed to disclose information from the System for Prediction of Environment Emergency Dose Information (SPEEDI). Some evacuees simply went to other parts of Fukushima Prefecture, which also received radioactive plume. It is not so cut-and-clean “evacuating Fukushima Prefecture quickly” type of business. Stable iodine was not administered to people other than one municipality, Miharu town, whose mayor bravely decided to administer it to the town residents against the advice of Fukushima Prefecture. Such details are often not included in the official documentation and not readily available to those seeking information from overseas.
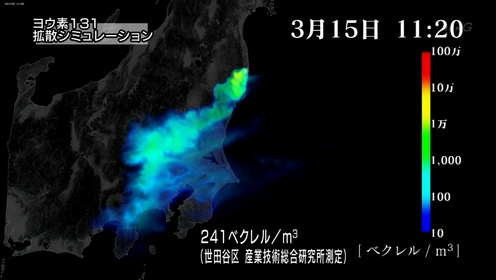
Actually, it is not just Fukushima Prefecture that received a significant amount of radiation contamination. The path of the plume went north and east initially, but then it turned south and covered a wide area including Tokyo and the surrounding Kanto region.
This is a recently broadcast simulation of iodine 131 using newly discovered data from a monitoring post located 5 km west of Fukushima Dai-ichi NPP. Tokyo received a radioactive plume, especially highly concentrated between 9am and 12pm on March 15, 2011.
However, the validity of the results of this study may be in question for a few reasons. First, internal radiation exposure was measured using a whole body counter (WBC), which only measures gamma radiation. Radioactive cesium actually emits beta radiation and decays to radioactive barium, which emits gamma radiation. Therefore, a WBC count, only including gamma radiation measurements, is not a true reflection of internal radiation exposure from all potential radionuclides which might have been released as a result of the accident. In addition, the detection limits were rather high at 210 to 250 Bq.
It is curious how Conca is encouraging consumption of still contaminated food, albeit how little or large, and resettlement of “only lightly contaminated areas.” The very same things have been pushed by the Japanese government in the name of “recovery” effort. In fact, Nikkei Newspaper, a major financial newspaper in Japan, published a full Japanese translation of Conca’s Forbes article online on January 17, 2013.
It is indeed curious that both Forbes and Nikkei Newspaper are “financial” publications. It appears that those whose interests are “finances” want to minimize health effects of radiation or radioactive contamination so that they can push their “peaceful” use of nuclear power, and they seem blind to the basic human rights of being able to breathe clean air and eat clean food.
He certainly seems excited about his specialty area of nuclear waste disposal, and at least Conca is correct in pointing out that decontamination effort that is passing for clean-up so far has been a huge waste of money by just moving dirt and leaves around. However, does he even know that some disaster debris with some degree of radioactive contamination is being transported all over Japan, at a great expense, to be incinerated? He probably doesn’t know, as he seems to spend very little time conducting research verifying facts prior to writing his articles.
Are the Japanese people being punished for some unspoken reason by having lower radiation levels in food? Is it really criminal to continue applying LNT dose effects for doses less than 100 mSv?
He is certainly entitled to having his own opinions, no matter how ”prevaricating” it sounds. (Conca himself used the word “prevaricating” in his article, stating that UNSCEAR needs to stop procrastinating and “prevaricating.”) However, observing the way he rants about “less than 100 mSv being nothing,” the infamous “Mr. 100 mSv” Shunichi Yamashita of Fukushima Medical University might have a newfound friend. And what is really criminal is to make Japanese people eat food contaminated with radiation no matter how little the contamination is, regardless of the “accepted global limits.”

